java File类的相关操作
本文共 527 字,大约阅读时间需要 1 分钟。
1.File类概述和构造方法
windows系统
- 一个点表示当前目录 直接写文件名字也是如此
- 两个点表示上级目录

注意第三个构造方法 父为对象 子为路径名

直接输出File对象会输出文件的绝对路径因为File类改写了toString()方法,输出时会自动调用
这三个构造方法做了同样的事情
2.File类的创建方法

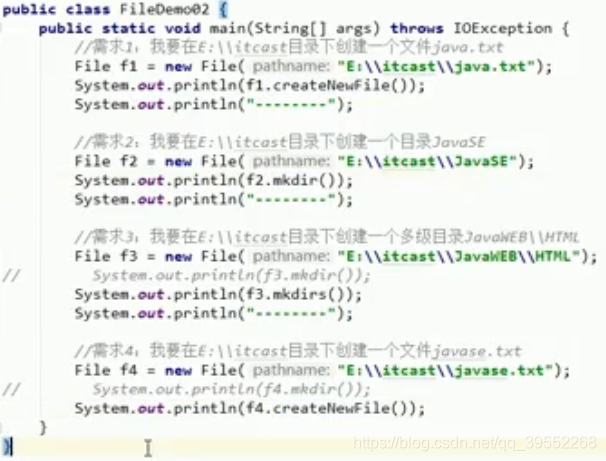
f4.mkdir()会创建一个名字为javase.txt的文件 如果这时再调用 f4.createNewFile会报false因为已经存在一个名字为javase.txt的目录,在这里目录就是文件的意思 mkdirs只能创建多层目录,如果想创建多层目录+txt文件就用mkdirs+creatNewFile

3.绝对路径和相对路径

4.delete和实例
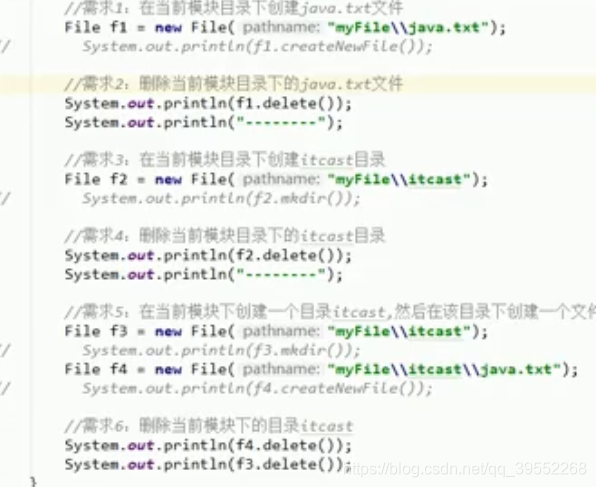
如果一个文件下有内容,则不能直接删除此文件
5.File常用方法
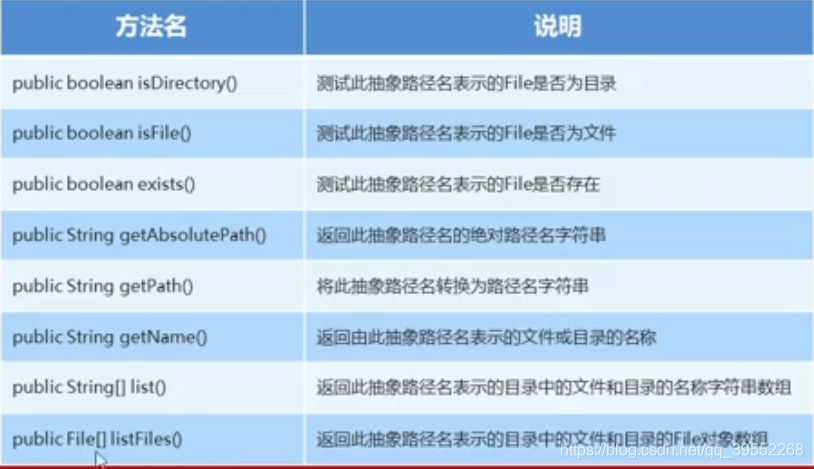 、
、
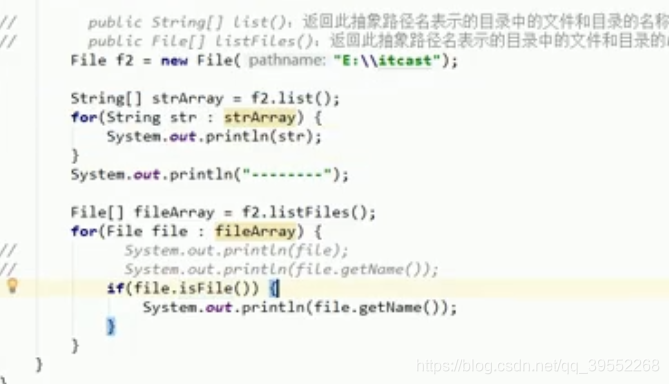
//抽象路径名 绝对路径名和 规范路径名的区别
file.list获取当前文件下的目录或文件的名字
就等于f2.listFiles()方法获取当前目录下所有文件和目录对象后在分别调用他们的getName()方法,但这个方法的好处就是可以通过文件对象来进行各种额外的判断操作如上面展示的
递归遍历一个目录下的所有文件

转载地址:http://ymsi.baihongyu.com/
你可能感兴趣的文章